우리 주변엔 시계열 데이터(time series) 데이터가 참 많다. 시계열 데이터를 다루는 방법도 그만큼 다양하게 발전해왔다. 이번에는 statsmodel 패키지의 seasonal_decompose()에도 쓰이는 Classical Seasonal Decomposition에 대해서 공부해봤다. 가장 먼저 개발된 방법인 만큼 한계가 분명하다. 공식 문서도 거의 쓰지 말라는 식으로;;(More sophisticated methods should be preferred) 명시할 만큼. 하지만 단순해서 널리 쓰이는 것도 사실이고, 이후에 개발된 더 정교한 모델들의 근간이 되는 모델이다. 아래 글들을 참고했다.

• Trend and Seasonalisty Decomposition 소개
• Classical(Naive) Decompostion의 방법과 한계

Components of Time Series

시간에 따라 변동하는 값을 나열한 데이터를 보면 규칙성을 찾고 싶어지는 것이 인지 상정. 사람들은 그래서 세 개의 요소로 시계열 데이터를 분해해서 생각하기로 했다.

• Level: 평균적인 값
• Trend: 일관적으로 상승 혹은 하락하는 추세
• Seasonality: 주기적으로 반복되는 패턴

위 세 요소는 시계열 데이터 중에서도 일관성과 규칙성을 띄는 부분이라 하여 systematic components라 불린다. 그런데 세상사가 그렇게 예측 가능하지만은 않다. 그 외에 다른 요소로 인한 노이즈는 non-systematic component라 한다. 다른 모델링과 마찬가지로 노이즈는 어쩔 수 없는 부분이다. 우리는 systematic components에 집중한다! 이렇게 분해함으로써 시계열 데이터에 대한 직관적인 이해가 가능해진다. 예를 들면 이 ‘기온은 점점 증가하는 추세구나!’ ‘교통사고는 7, 8월에 일관적으로 상승하는구나!’ 같은 식으로. 또한 추후의 모델링의 정확도를 제고하는데 활용할 수도 있다. 예를 들면, explicit하게 데이터에서 모델링한 트렌드의 값을 빼서 time series 내 트렌드의 영향력을 제거한 뒤 다른 변수의 영향을 살펴볼 수 있다¹. 넷플릭스 챌린지에서 사람들이 시간이 지날 수록 평이 후해진다는 trend를 발견하고 이를 bias의 term으로 추가한 것이 좋은 예시.

Additive vs Multiplicative

우리는 타임시리즈의 각 데이터 포인트를 level, trend, seasonality 그리고 noise의 조합으로 나타낼 수 있다. 그 조합은 덧셈일 수도, 곱셈일 수도 있다. 데이터를 ploting하거나 기본적인 기술 통계를 활용해 둘 중에 적절한 모델을 선택한다. (물론 정 모르겠으면 둘 다 해보고 사후적으로 평가하는 방법도 가능하다!)

	Applicative Model	Multiplicative Model
Model	\(\hat y(t) = Level + Trend + Seasonality + Noise\)	\(\hat y(t) = Level * Trend * Seasonality * Noise\)
특성	시간에 따른 변화가 일정하다	quadratic, exponential 등의 모양을 취하며 시간에 따른 변화폭이 커지거나 작아진다
Trend	선형적인 상승/하락 추세	비선형적인(curved) 상승/하락 추세
Seasonality	frequency(주기)와 amplitude(변화폭)이 일정하다	frequency(주기)와 amplitude(변화폭)이 커지거나 작아진다

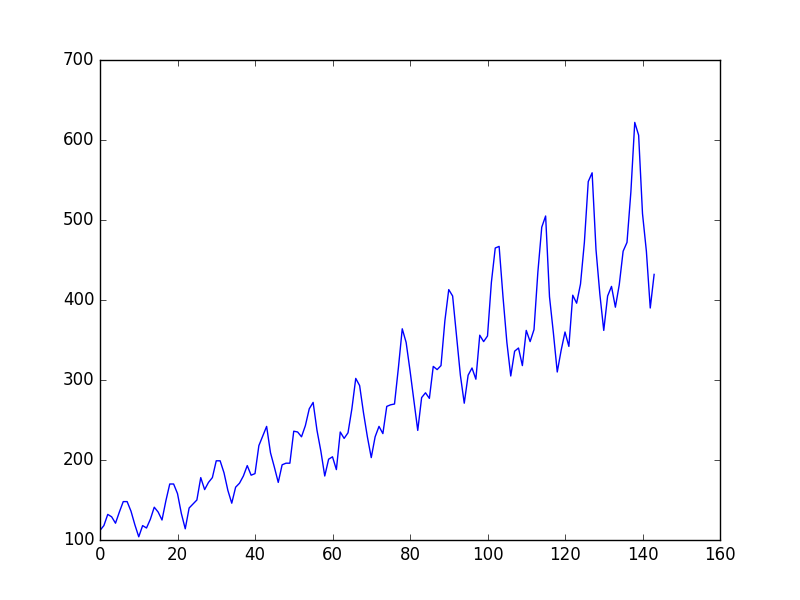시간의 흐름에 따른 항공기 이용객의 수. 사이클의 크기가 점점 커지고 있으니 multiplicative model이 적절하다

주기적 변화의 크기나 전체적인 level을 기준으로 한 variation이 일정할 때에는 additive decomposition이 적절하다. 만약 이들이 시간의 흐름에 비례하게 변화한다면 multiplicative decomposition을 고려해봐야 한다. 특히 경제 지표 관련 타임시리즈는 multiplicative model을 따르는 경우가 많다².

차근차근 Classical seasonal decomposition

그래서 덧셈이든, 곱셈이든 어떻게 분해할 건데? 그 방법이 곧 seasonal decomposition이다. 가장 먼저 개발된 classical(naive) decomposition은 모델이라기 말하기도 민망할 만큼 덧셈과 뺄셈(혹은 곱셈과 나눗셈) 몇 번이면 뚝딱 trend와 seasonality를 분리해낸다. Moving Average로 trend를 측정하고, trend를 원 데이터에서 제거하여 seasonality를 도출한 뒤, seasonality를 0점 조정하면 끝!

Trend Component: Moving Average

Moving Average(MA)는 말 그대로 일정한 크기의 윈도우를 움직여가며 관측치들의 평균을 측정하는 것이다. 예를 들면 t번째 시간의 order = 5 인 MA는 앞선 2개 period의 관측치와 t일때의 관측값, 뒤 따라오는 2개 period의 관측값의 평균이다. 이런식으로 개별 관측값들의 randomness를 완화하여 전반적인 추세를 도출할 수 있다. 윈도우가 움직이는 것을 상상해보면 쉽다. 하나의 관측치는 윈도우 안에 서서히 들어왔다가 서서히 빠져나간다. 개별 관측치들의 영향력은 여러 평균 값에 걸쳐 분산되고 부드러운 추세선을 얻을 수 있다. 아래 그림처럼 삐죽빼죽했던 연도별 전기장비 제조 규모 데이터에 대해서 12-MA를 취하면 전반적인 추세만을 부드럽게 그려 낼 수 있다.

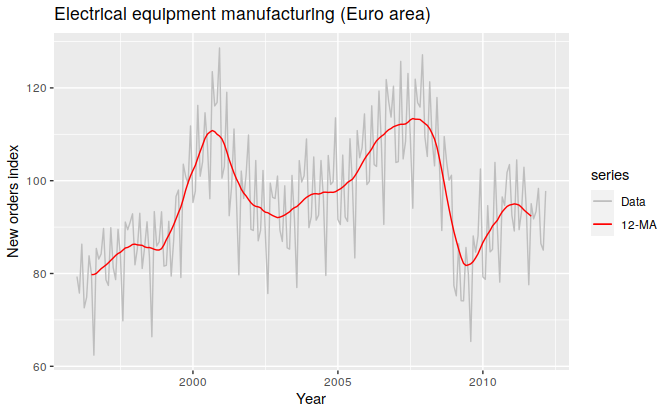연도별 전기장비 제조 규모 원 수치와 moving average로 도출한 추세선

order의 크기는 time series에서 설정한 period의 주기에 따라 결정한다. weekly data라면 7로, quarterly data라면 4로 설정하는 것. 하지만 quarterly data 처럼 주기가 짝수인 경우, 윈도우 내에서 시간 t 이전 데이터와 이후 데이터의 개수가 달라지는 문제가 발생한다. 윈도우 내 이전 데이터와 이후 데이터의 영향력을 대칭으로 유지하기 위해 이렇게 도출한 MA에 다시 한 번 2-order MA를 취함으로써 이를 방지할 수 있다. 이렇게 측정한 추세가 바로 트렌드에 대한 예측치 \(\hat T_{t}\)가 되겠다!

Seasonal Component

그 다음은 쉽다! 우선 trend를 제거한 데이터(detrended series)를 도출한다. 각 월별로 seasonality를 도출하는 상황이라면 3월의 detrended value 끼리 모은 뒤 평균을 내면 된다. Additive Model이라면 \(y_{t}-\hat T_{t}\), Multiplicative 라면 \(\frac{y_{t}}{\hat T_{t}}\)가 되겠다. 그리고 각 주기마다 trend를 제거한 데이터의 평균을 내면 해당 주기의 영향력 \(\hat S_{t}\) 가 된다. 여기서 각 주기의 seasonality는 trend에 대한 상대적인 증가 혹은 감소를 나타내므로 합이 0이 되도록 조정된다.

Residual 잘 살피기

residual은 말 그대로 원 데이터에서 앞서 도출한 trend와 seasonality의 값을 제거한 나머지 값이다. 모델의 규칙성 내에 포착되지 않은 데이터를 말하는데, 이를 통해 우리는 모델이 데이터의 값을 포착하는데 적절한지 가늠해볼 수 있다.
예를 들면 residual로 classic seasonal decomposition 중에서도 additive 모델이 적절한지, multiplicative 모델이 적절한지 확인해볼 수 있다. 아래 그래프는 구글의 주가 변동에 대해 additive seasonal decomposition과 multiplicative seasonal decomposition을 시행한 결과이다. 물론 경제 지표들은 변화의 폭이 선형적으로 증가한다는 일반론이 있지만, 원데이터를 보고 가늠하기란 쉽지 않다. 이 때 두 방법론을 모두 실행해 residual을 보면 multiplicative decomposition의 결과가 현저히 작은 것을 확인할 수 있다.(물론 residual이 작은 것이 항상 성공적인 모델링을 보장하는 것은 아니다. 노이즈를 패턴으로 인식하여 엉뚱한 결과가 나올수도 있다.)

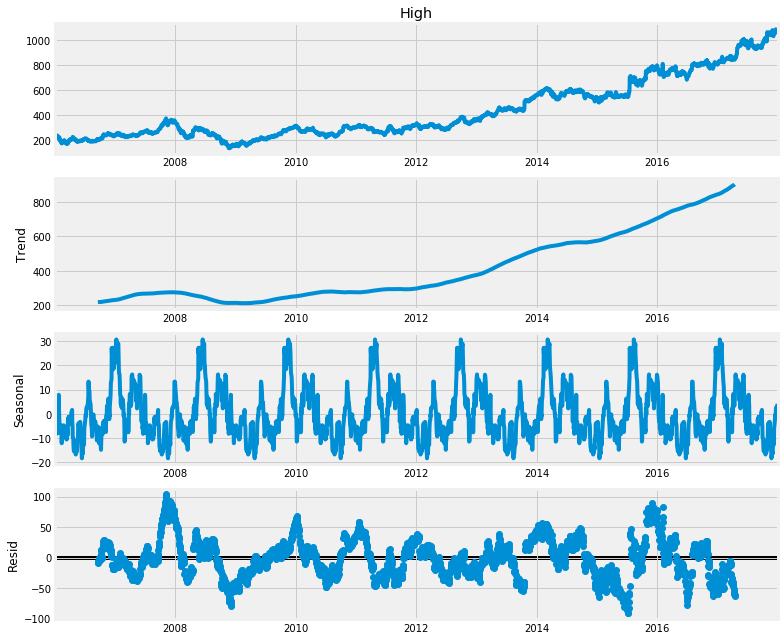구글 주가 변동에 additive seasonal decomposition을 시행한 결과

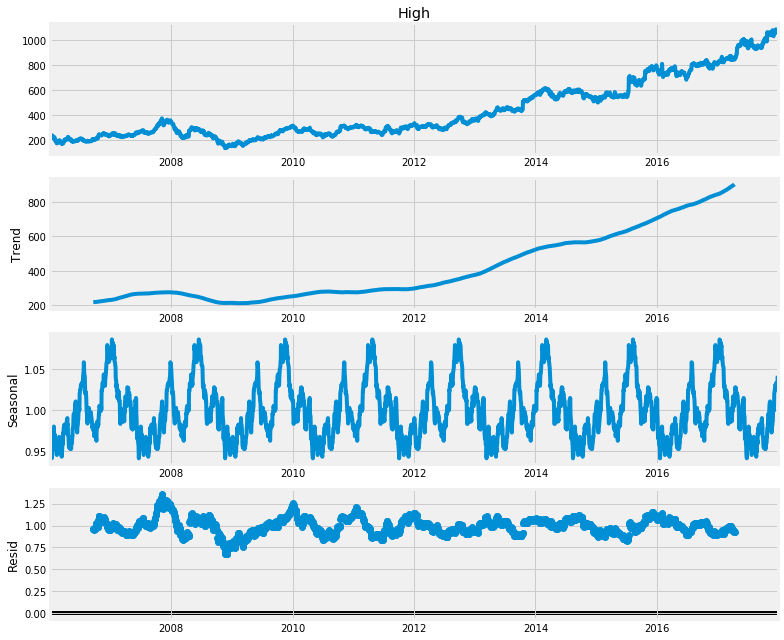구글 주가 변동에 multiplicative seasonal decomposition을 시행한 결과

또 다른 예시는 residual로 데이터의 누수(leakage)가 있는지 확인할 수 있다. 아래 그래프를 보면, 2009년 이후 1 이하의 값들이 그 전과 다른 양상을 띄며, 그 내에서 점점 줄어드는 나름의 규칙성을 띈다. 모델 내부의 규칙성으로 설명되어야할 값들이 노이즈로 취급되어 모델에 반영되지 못하는 상황이다. 이는 주기 별 seasonality가 일관적이라고 가정하는 classical decomposition의 한계에서 비롯한 것으로, 다른 decomposition 방법론을 필요로 한다.

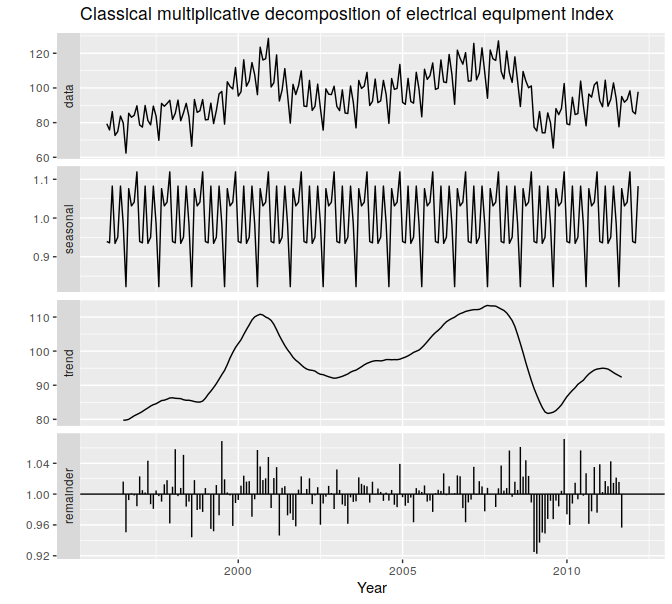전기 장비 제조량에 multiplicative decomposition을 시행한 결과. 2009년 이후 remainder(residual)에 주목

한계

앞선 예시에서 절절하게 와닿는 나이브함… 그 배경은 주기마다 seasonal component가 동일하다고 전제하는 데에 있다. 엥 multiplicative decomposition에서는 시간에 따라 변화의 폭이 변할 수 있는데요? 아니다. 이 또한 일정한 계수(coefficient)를 가정한다. classical decomposition에서 seasonality를 도출하는 과정의 핵심은 어쨌든 detrended value의 평균을 내는데 에 있다. 그래서 앞선 전기 장비 제조량의 예시에서처럼 에어컨 등의 보급으로 그 전과 질적으로 다른 요소가 시계열 데이터에 영향을 미칠 경우 이 변화를 포착할 수 없다.
또 다른 치명적인 한계는 최초 관측량과 최근 관측량에 대해서는 trend 및 seasonality를 측정할 수 없다는 점이다. Moving Average의 원리를 생각해보면 간단하다. 앞 뒤 정해진 횟수의 관측치와 함께 평균을 내야하는 데, 최초 관측치는 그보다 선행하는 관측치가 없기 때문에 MA를 도출하지 못한다는 간단한 이야기. 사실 classical decomposition은 아직도 널리 쓰이지만, 텍스트북이며 공식 도큐먼트며 조금만 진지한 아티클을 찾아보면 쓰지 말라고 성화다. X11이나 SEATS, STL 등 그 이후에 개발된 많은 decomposition 들을 활용하자는 것. classical decomposition이 나온지 100년(..)이 되었으니 그럴만하다.